▪ CNDD常用中介变量数据推荐:
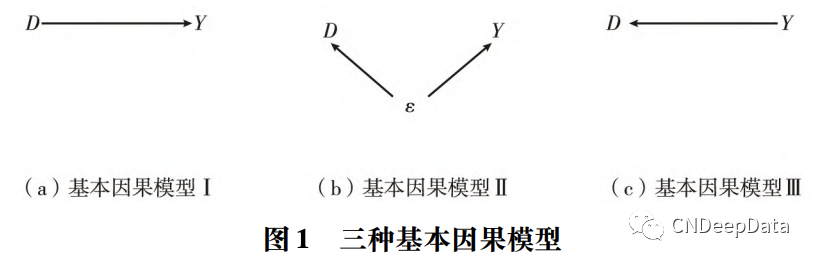
Y 表示研究所关注的结果(Outcome) 、反应( Response) 或被解释变量, D 表示有待考察的、导致结果发生的原因(Cause) 、处理( Treatment) 或核心解释变量。图1展示了三种基本因果模型。模型 I 刻画了基本因果关系。模型 II 表明,这种相关性可能是因为存在第三方混淆因素( Confounding Factor) 同时影响 D 和 Y。模型 III 则表明,这种相关性可能是因为 Y 对 D 的反向影响( Reverse Causality) 。
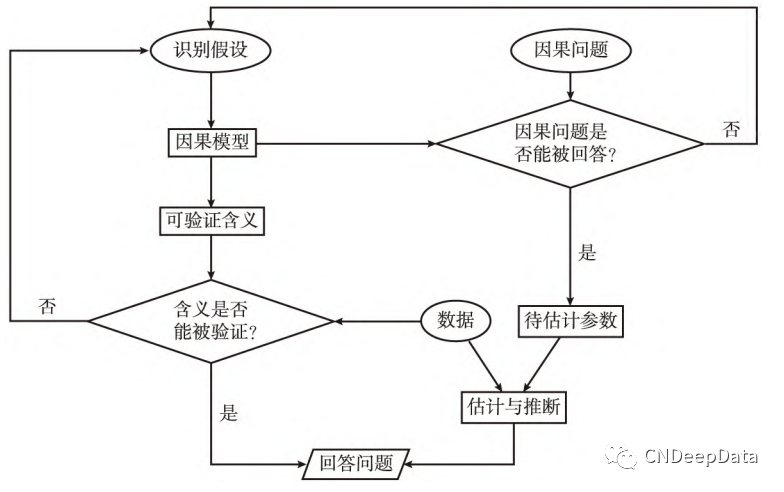
如果在特定的研究情境下,变量之间满足一定的假设条件,使得一个特定的因果模型没有与之竞争的、观测上等价 ( Observationally Equivalent) 的因果模型,则称这个特定的因果模型被识别,这样的假设被称作识别假设。
▪ 因果识别的策略
因果识别有两种基本策略。第一种基本识别策略是寻找特定的研究情境。识别的基本逻辑是如果相关性不存在,则因果性不存在; 如果相关性存在且只有一种因果模型可以合理化这种相关性,则这种特定的因果性存在。
第二种基本识别策略———挖掘因果模型更丰富的、可验证的相关性含义( Testable Implications) ,即提出这样的问题: 如果从 D 到 Y 的因果关系真的存在,那么还将观测到何种现象? 不同的因果模型对新的相关性可能给出不同的预测,由此通过打破其在观测上的等价性来达到用数据验证 模型的目的。
中介效应是指原因通过一个或几个中间变量影响结果,这种中间变量被称作中介变量 (Mediating Factor,或简称 Mediator) 。一组因果关系及其作用渠道可以用如下结构模型来刻画:

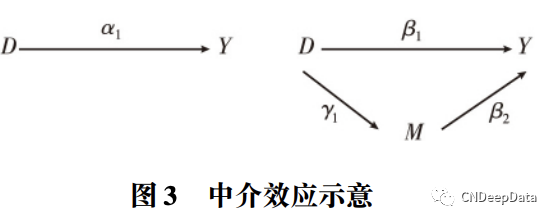
假定 D 是一种随机处理,即 E( εY1D) = 0 和 E( εMD) = 0 成立,因此,(1) 式和(3) 式的普通最小二乘估计分别能够得到 α1 和 γ1 的一致估计:

在(2) 式的普通最小二乘估计中,根据 Frisch-Waugh-Lovell 定理,有:
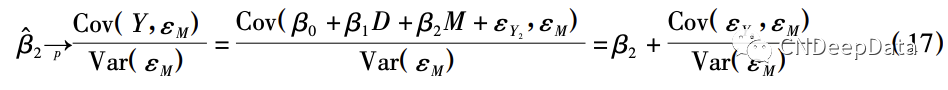
其中,第二个等号用到 Cov( εM,D) = 0 以及 Cov( M,εM ) = Var( εM ) 。将( 3) 式代入(2) 式,有:
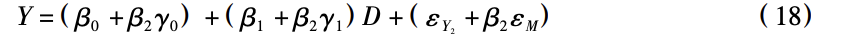
可知 α0 = β0 + β2γ0,α1 = β1 + β2γ1,εY1 = εY2 + β2εM。特别地,有:
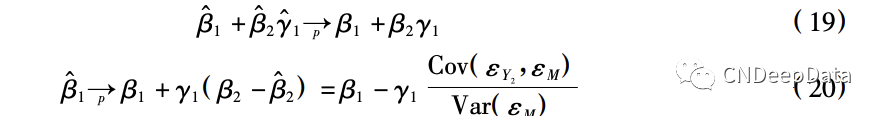
因此,只有当
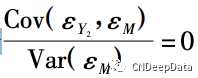
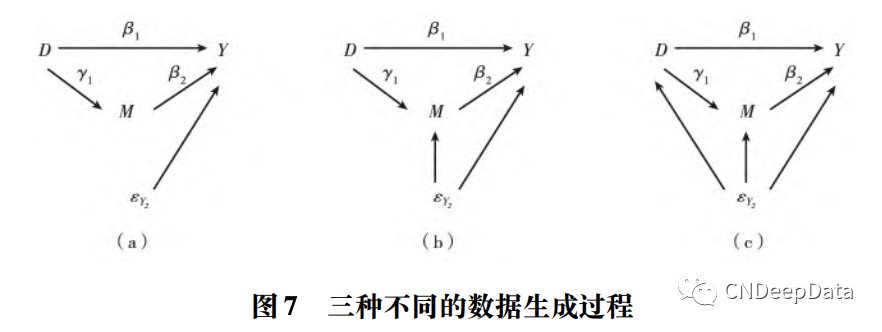
在以处理观测性数据为主的经济学因果推断研究中,研究者面临着更富有挑战性的处境: 真实的数据生成过程很可能如图 7(c) 所示。此时处理变量的生成方式不再来自于研究者外生的实验干预,而来自于研究对象的主动选择,因此,研究者在研究设计上的努力主要聚焦在如何解决处理变量的内生性问题,中介变量的内生性问题不得不成为等而次之的问题。或者说,解决处理变量的 内生性并探究其对结果的影响,同解决中介变量的内生性并探究其对结果的影响,应该成为两项独立研究各自的主题,以确保每项研究都聚焦在一个核心解释变量上。除非能够从理论上证明并不 存在同时影响中介变量和结果变量的混淆因素,或者能够良好地定义、充分地穷举和准确地测度这 些混淆因素并且方便地将其作为控制变量放入(2) 式中,否则这种回归并不能产生任何增进我们理解 D→M→Y 这一因果链条的有益知识。
上文的讨论表明,中介效应检验的适用前提是,识别 D 对 M 和 Y 的因果关系比较容易,同时识别 M 对 Y 的因果关系也比较容易。而对于观测性数据研究,真实的数据生成过程纷繁复杂,找到合适的研究情境来研究 D 对 Y 的因果关系已属不易,研究中介效应更是困难,这就是为什么中介效应检验历来在经济学经验研究文献中很少见的主要原因。
中介效应检验不可靠,并不意味着不研究因果关系的作用渠道。一种常见的做法是,提出一个或 几个中介变量 M,这些变量和 Y 的因果关系在理论上比较直观,在逻辑和时空关系上都比较接近,以 至于不必采用正式的因果推断手段来研究从 M 到 Y 的因果关系; 然后仅看 D 对 M 的影响,即只考察 ( 1) 式和( 3) 式,而不考察( 2) 式,从而避免正式区分出在间接效应之外是否还有无法解释的直接效应。
关于中介效应分析,文章提出以下操作建议: 一是停止使用中介效应的逐步法检验,更不需要估计间接效应的大小并检验其统计显著性。把研究的重心重新聚焦到如何提高 D 对 Y 的因果关系的识别可信度。二是根据经济学理论,提出一个或几个能够反映 D 对 Y 的作用渠道的中介变量 M, M 对 Y 的影响应该是直接而显然的,采用和第一条中同样的方法识别 D 对 M 的因果关系。三是尽 避免提出与 Y 的因果关系不明显、因果链条过长或者明显受到 Y 反向影响的中介变量。有时,考 察 Y 对 M 的回归也许是有益的,但要记住这只是一条相关性证据。四是在绝大多数时候,做好前两条就足够了。如果要考察 D 对 Y 的效应在多大程度上可以被 M 这一作用渠道所捕捉,可以尝试在 Y 对 D 的回归中控制 M,但必须先弄清楚这种考察对理解 D 对 Y 的因果关系有何帮助,并审慎解释回归结果。如有可能,尽量论证这一结果受到 M 的潜在内生性的影响是有限的。当存在多个 M 时,尤其要谨慎采用这种做法。
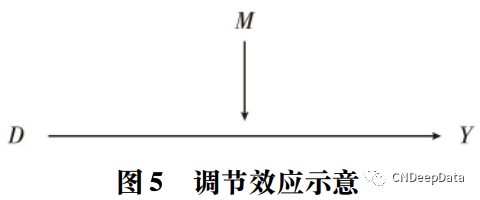
调节效应是指原因对结果的影响强度会因个体特征或环境条件而异,这种特征或条件被称作调节变量 ( Moderating Factor,或简称 Moderator) ,如图 5 所示。交互项模型是对调节效应进行建模的主要方式。
(1) 两个处理变量的情形。构成交互项的两个解释变量都是核心解释变量:
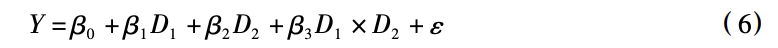
两个核心解释变量对 Y 的边际效应分别为:
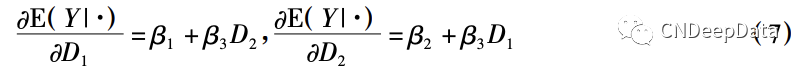
此时,较少说两个核心解释变量互为调节,而是说该模型适用于考察两个变量对 Y 影响的互补性( β3 > 0) 或替代性( β3 < 0) 。
(2) 一个处理变量的情形。在大多数时候,一项因果推断研究只关注一个处理变量,仍记作 D, 将调节变量记作 M,则有:
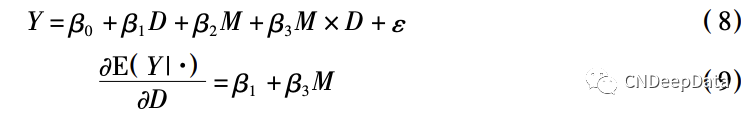
此时称 D 对 Y 的因果影响受到 M 的调节: 如果 β3 > 0,则 D 对 Y 的正面影响随着 M 的增大增强( 或负面影响随着 M 的增大而减弱) ; 如果 β3 < 0,则 D 对 Y 的正面影响随着 M 的增大而减弱 (或负面影响随着 M 的增大而增强) 。
如果 β3 在统计上显著,则称观测到了显著的调节效应。但 β1 的大小和统计显著性是否具有经济意义,要视具体的研究情境而定,因为此时 β1 的含义是当 M = 0 时 D 对 Y 的因果效应。很有可能当 M = 0 时 D 对 Y 影响不显著,才是符合理论预期的。
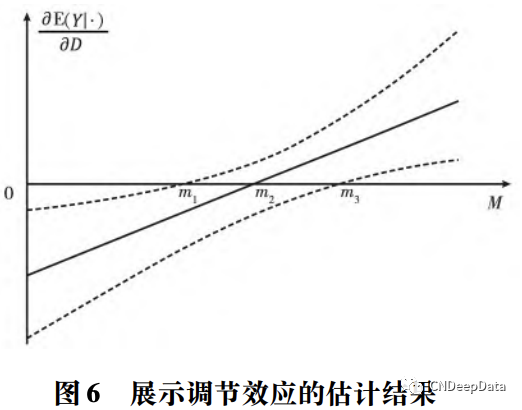
除了报告系数的估计结果之外,通常还会根据需要,报告因果效应的一个或几个估计值(以及标准误、置信区间、显著性检验的 p 值等) 。如图 6 所示。在这个示意图中,β1 < 0,β3 > 0,实线表示因果效应的估计值,虚线表示给定置信水平的置信区间。当 M < m2 时,D 对 Y 的因果效应是负向的; 当 M < m1 时,这种负向效应在统计上显著; 当 M > m2 时,D 对 Y 的因果效应是正向的; 当 M > m3 时,这种正向效应在统计上显著。
(3) 调节变量为虚拟变量的情形。当调节变量 M 为虚拟变量时,还可以把交互项模型等价地理解为分组回归:
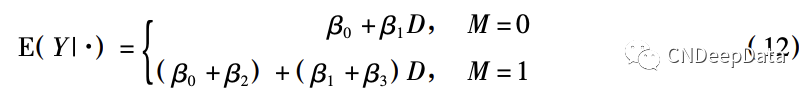
换言之,分组回归下 D 对 Y 的因果效应的组间异质性可以通过交互项模型来检验,即表现为交互项 M × D 系数估计的统计显著性。这种检验总是有必要的,因为组间异质性不能诉诸于直观判断。例如,D 对 Y 的因果效应在 M = 0 组是不显著的,在 M = 1 组是显著的,但它们之间的差异很可 能是不显著的。
有时为方便展示结果,对(8) 式进行如下等价变换:
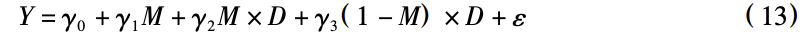
此时 γ2 和 γ3 分别是 M = 1 组和 M = 0 组的 D 对 Y 的因果效应。
因此,当调节变量为虚拟变量时,有三种呈现结果的方式。第一种是报告( 8) 式的结果,这种方式的好处是直接显示了 D 对 Y 的因果效应的组间异质性,缺陷是 M = 1 组的因果效应没有直接显示。第二种是分组报告(12) 式的结果,这种方式的好处是直接显示了这两个组的因果效应,缺陷是因果效应的组间异质性检验还需要额外通过( 8) 式来实现。第三种是报告(13) 式的结果,这种方式的好处也是直接显示了这两个组的因果效应,因果效应的组间差异虽然没有直接显示,但是可以 便地通过检验 H0 ∶ γ2 = γ3 来实现。
(4) 处理变量和调节变量均为虚拟变量的情形。当处理变量 D 和调节变量 M 均为虚拟变量时,交互项系数有一种方便的理解: 处理组( D = 1) 与控制组( D = 0) 的结果均值的组间差异之差异,简称双重差分( Difference in Differences) 。对于(8) 式,易知:
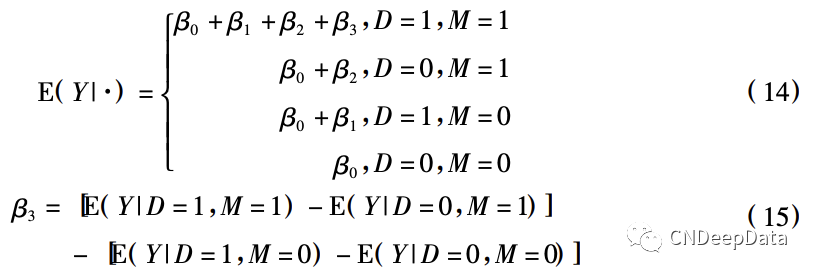
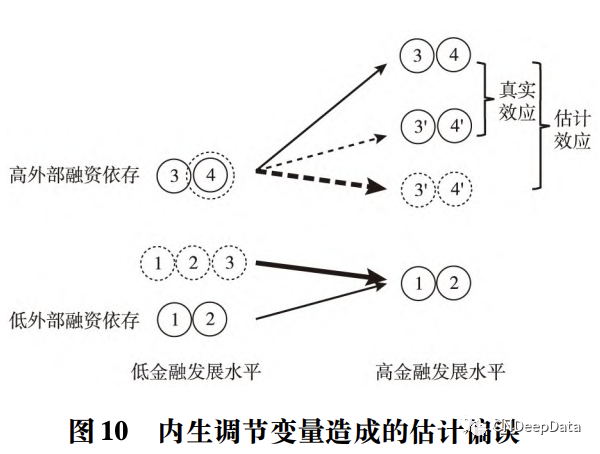
例如,Y 表示工资水平,D 表示是否上大学,M 表示是否为男性,则 β3 表示男性的上大学回报率与女性的上大学回报率的差异。特别地,当 D 为处理实施后的虚拟变量,M 为是否最终接受处理的虚拟变量,这种特殊的调节效应模型就是双重差分模型。反过来说,无论 D 和 M 是离散变量还是连续变量,无论其变动性是截面维度还是时间维度,交互项系数都应该在双重差分的意义下去理解。这里涉及的一个具体问题是,如何在双重差分的意义下表述交互项系数的经济含义。当 D 和 M 均为虚拟变量时,含义的表述比较方便: β3 表示处理的实施对结果的影响。当 M 为连续变量时, 意味着所有个体都接受了处理,只是处理的强度( Treatment Intensity) 有所不同,此时含义可以表述 为: 当 M 增加一个标准差 σM 时,处理的实施对结果的影响会提高 σM·β3。当 D 和 M 均为连续变量 时,表述尤其需要小心。Rajan and Zingales( 1998) 使用跨国行业层面数据研究金融市场的发展是否影响产业增长。D 为反映一国金融发展水平的指标,M 为反映某一行业外部融资依存度的指标, Y 为该国该行业增加值的增长率。β3 > 0,表明更加依赖于外部融资的行业,在金融市场发展水平 越高的国家增长得更快。研究结果的经济含义是: 在样本中,典型的高外部融资依存行业是 M 居 于 75 分位的机床业,典型的低外部融资依存行业是 M 居于 25 分位的饮料业,典型的高金融发展水平国家是 D 居于 75 分位的意大利,典型的低金融发展水平国家是 D 居于 25 分位的菲律宾,因此, 相较于菲律宾,在意大利机床业的增长比饮料业要快 β ^ 3 ·( M75 -M25 )·( D75 -D25 ) ,然后将这一数字与 Y 的样本均值进行比较,表明其足够大以至不可忽略。
调节效应分析和异质性分析这两者是一回事。最简单的理解: 当调节变量 M 是虚拟变量时, 相当于把全样本分为 M = 0 和M = 1两个组,交互项 M × D 的系数就是分组进行的 Y 对 D 的回归中 D 的系数的组间异质性。当 M 是连续变量时,本质上并没有发生变化,D 对 Y 的因果效应受到 M 的调节,也就是可以理解为,D 对 Y 的因果效应在高 M 组和低 M 组之间存在异质性。
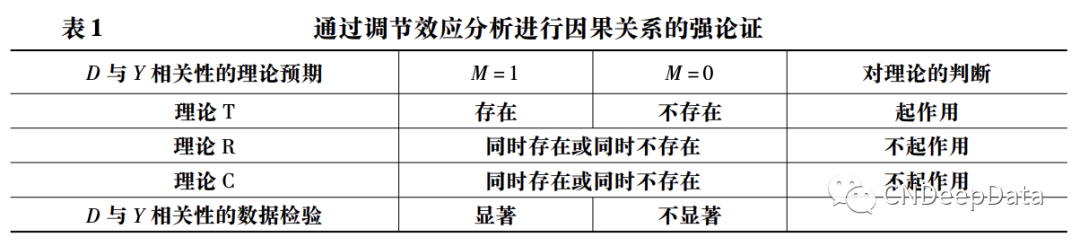
有时两组中 D 与 Y 的相关性都存在,但在 M = 1 组这种相关性更强,表现在 Y 对 D 的回归中 D 的系数估计绝对值在 M = 1 组更大,且组间差异在统计上显著。这时至少可以说,D 与 Y 的相关性不全是理论 R 或理论 C 所带来的,否则这种相关性应该在 M = 1 和 M = 0 组无差异。这样尽管没有证伪理论 R 或理论 C,但至少证实了理论 T,也在因果论证上迈出了一大步。这一弱论证的逻辑可 以通过对表 1 稍作修改来总结,如表 2 所示。
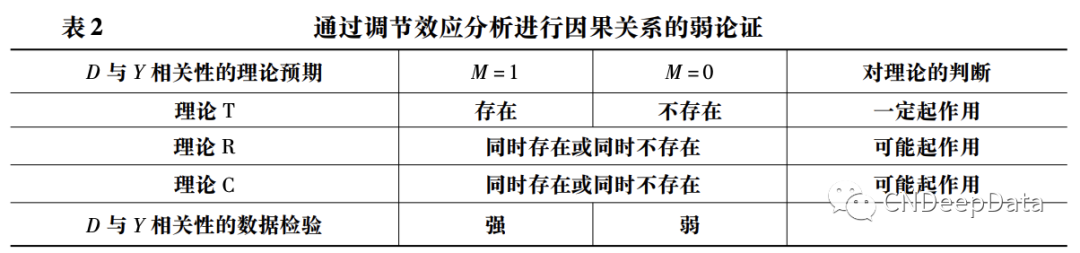
▪ 调节效应分析的操作建议

版权声明 …
1. 除中国深度数据库(CNDD)特殊声明外,CNDD对基于合法来源的数据的选择、整理和编排具有独创性。任何自然人、法人、其他组织未经CNDD授权,不得以任何目的截取、上传、下载、复制、修改、使用、编译等或者以任何方式任何媒介传播上述作品的任何部分,否则视为侵权。
2. 对于存在侵害CNDD上述权利违法行为的主体,CNDD保留依法追究其法律责任的权利。
数据授权使用说明 …
任何使用CNDD数据等产品的单位和个人,承诺只将CNDD的数据等用于学术研究,并在所得研究成果(包括但不限于学术论文、咨询报告等)中注明数据来源于CNDD。数据来源的注明方式请参考:“本研究数据来源于中国深度数据库CNDD”;英文参考:“We get the data from CNDeepData (CNDD)”。

CNDeepData:Let high-quality data flow without barriers
部分图片来源于网络,如涉侵权请告知,本站将第一时间删除。客服微信号:DeepData001